为什么“最难”与“未解”常被并列?
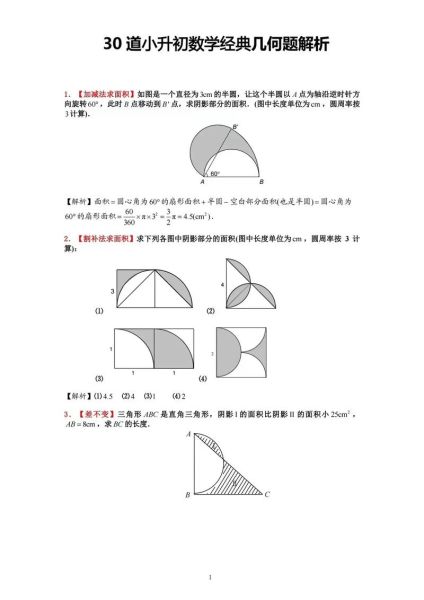
在搜索引擎里,“数学史上最难的题有哪些”与“至今未解的数学难题”这两个长尾词总是成双出现。原因并不复杂:大众既想知道历史上曾让天才折腰的经典,也关心今天仍悬而未决的问号。下面用自问自答的方式,把两者拆开揉碎,一次讲透。

哪些题目曾被称为“史上最难”?
1. 古希腊三大几何难题
- 化圆为方:仅用圆规与无刻度直尺,把给定圆变成等面积正方形。
- 倍立方:构造体积为原立方体两倍的立方体。
- 三等分角:将任意角三等分。
19世纪,伽罗瓦理论与林德曼证明π的超越性,让这三题被彻底判死刑:在尺规限制下无解。
2. 费马大定理
“当n>2时,xⁿ+yⁿ=zⁿ无正整数解。”这条写在书页边缘的句子折磨了数学家358年,直到1995年怀尔斯用椭圆曲线与模形式将其终结。
3. 四色问题
“任何地图只需四种颜色即可相邻区域不同色。”1976年,阿佩尔与哈肯用计算机枚举了1936种构型,首次把机器证明带进主流视野。
至今未解的数学难题清单
1. 黎曼猜想
非平凡零点实部是否全为1/2?这条假设连接了素数分布与复分析,被克雷数学研究所列为“百万美元问题”之首。
2. P vs NP
多项式时间内可验证的问题是否也能多项式时间内解决?密码学、算法优化、人工智能全被它牵着鼻子走。
3. 纳维-斯托克斯方程的光滑解
描述流体运动的这组偏微分方程,在三维空间中是否存在全局光滑解?飞机设计、天气预报都在等答案。
4. BSD猜想
椭圆曲线有理点群的秩与L函数在1处的零点阶数是否相等?它把代数几何与解析数论缝在一起。
5. 霍奇猜想
一个复杂的高维几何对象,其“洞”的拓扑信息能否由代数方程完全描述?这是代数几何的心脏手术。
这些难题为何如此顽固?
技术门槛:工具尚未发明
以黎曼猜想为例,现有复分析工具无法跨越临界线的鸿沟。数学家自嘲:“我们像在夜里丢钥匙,却只在路灯下找。”
计算极限:暴力枚举不可行
P vs NP若成立,意味着所有NP问题都能被“快速”解决;但穷举搜索空间呈指数爆炸,今天的超级计算机也束手无策。

概念黑洞:定义本身模糊
纳维-斯托克斯的光滑解问题里,“光滑”一词在三维湍流中缺乏统一量化标准,导致攻击路线四分五裂。
普通人如何参与这些难题?
1. 从科普到专业:阶梯式阅读
- 入门:《素数的音乐》(黎曼猜想)
- 进阶:《计算不可行性》(P vs NP)
- 高阶:原始论文+arXiv预印本
2. 分布式计算:贡献CPU算力
PrimeGrid、GIMPS等项目让爱好者把电脑空闲时间变成素数猎人,曾帮助发现第51个梅森素数。
3. 形式化证明:Lean与Coq
开源证明助手Lean正在尝试形式化BSD猜想的部分结果,程序员可提交代码片段,成为“逻辑搬砖工”。
未来十年哪些难题可能突破?
1. 黎曼猜想的“量子化”路线
物理学家发现随机矩阵特征值分布与零点统计惊人吻合,量子混沌理论或成突破口。
2. P vs NP的“电路下界”
2023年,Ryan Williams提出非均匀电路复杂度新框架,被视作近20年来最接近的一次冲锋。
3. 纳维-斯托克斯的“计算机辅助反例”
陶哲轩团队用机器学习搜索近似解,发现可能产生有限时间爆破的初始条件,正逼近严格证明。
常见误区澄清
误区1:解决难题只靠天才
怀尔斯证明费马大定理时,整合了椭圆曲线、模形式、伽罗瓦表示三大领域成果,团队协作同样关键。
误区2:计算机证明不算数学
四色问题的机器证明引发哲学争议,但形式化验证已让计算机成为数学家的“第二支笔”。
误区3:难题无用
RSA加密直接源于大整数分解难题,而量子计算对RSA的威胁又催生了后量子密码学,形成“问题—应用—新问题”的循环。
写在最后的追问
如果明天黎曼猜想被证明,世界会怎样?素数分布公式将彻底改写,密码体系需连夜升级;如果P=NP,区块链可能瞬间崩塌,药物设计却迎来黄金时代。未解难题像一面镜子,照出人类认知的边界,也映出下一个文明跃迁的入口。

评论列表